Diagonal of a Box Calculator

Length (\( L \)):

Width (\( W \)):

Height (\( H \)):

1. What is Diagonal of a Box Calculator?

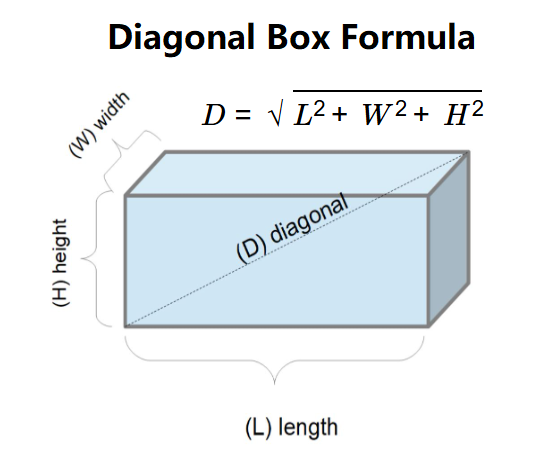
Definition: This calculator computes the diagonal (\( D \)) of a rectangular cuboid (box), which is the straight-line distance from one corner to the opposite corner through the interior of the box.

Purpose: It helps in determining the longest straight-line distance inside a box, useful for packaging, shipping, and design applications to ensure items fit diagonally.

2. How Does the Calculator Work?

The calculator uses the following equation:

\( D = \sqrt{L^2 + W^2 + H^2} \)

Where:

\( L \): Length of the box (in any unit);
\( W \): Width of the box (in any unit);
\( H \): Height of the box (in any unit);
\( D \): Diagonal of the box (in selected result unit);
Results are displayed with 3 decimal places (or scientific notation if less than 0.001).

Steps:

Enter the length (\( L \)) of the box and select the unit (in, ft, yd, mm, cm, m).
Enter the width (\( W \)) of the box and select the unit (in, ft, yd, mm, cm, m).
Enter the height (\( H \)) of the box and select the unit (in, ft, yd, mm, cm, m).
Click "Calculate" to compute the diagonal.
Change the result unit dropdown to convert the diagonal value to a different unit.

3. Importance of Diagonal of a Box Calculation

Calculating the diagonal of a box is crucial for:

Packaging and Shipping: Ensures that items fit diagonally within a box, especially for long objects like poles or pipes.
Design and Manufacturing: Helps in designing boxes or containers to accommodate specific items.
Space Optimization: Assists in determining the maximum size of an object that can fit inside a box without exceeding its diagonal length.

4. Using the Calculator

Example 1: Calculate the diagonal of a box with \( L = 10 \, \text{in} \), \( W = 5 \, \text{in} \), \( H = 3 \, \text{in} \), result in in:

Length: 10 in;
Width: 5 in;
Height: 3 in;
\( D = \sqrt{10^2 + 5^2 + 3^2} = \sqrt{100 + 25 + 9} = \sqrt{134} \approx 11.576 \, \text{in} \);
Result: Diagonal = 11.576 in.

Example 2: Calculate the diagonal of a box with \( L = 1 \, \text{m} \), \( W = 50 \, \text{cm} \), \( H = 30 \, \text{cm} \), result in cm:

Length: 1 m (39.3701 in);
Width: 50 cm (19.685 in);
Height: 30 cm (11.811 in);
\( D = \sqrt{39.3701^2 + 19.685^2 + 11.811^2} \approx \sqrt{1549.99 + 387.5 + 139.5} \approx \sqrt{2076.99} \approx 45.574 \, \text{in} \);
Convert to cm: \( 45.574 \times 2.54 \approx 115.759 \, \text{cm} \);
Result: Diagonal = 115.759 cm.

5. Frequently Asked Questions (FAQ)

Q: What is the Diagonal of a Box?
A: The diagonal of a box is the straight-line distance from one corner to the opposite corner through the interior, calculated using the lengths of its three dimensions.

Q: Why is the diagonal important?
A: The diagonal determines the longest straight-line distance inside a box, which is critical for fitting long objects or ensuring proper packaging.

Q: Can I use different units for each dimension?
A: Yes, the calculator allows you to select different units for length, width, height, and the result, converting all inputs internally for accurate calculation.