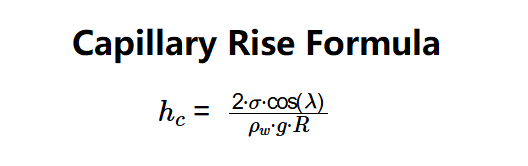Capillary Rise Calculator

Surface Tension (\( \sigma \)):

Meniscus Angle (\( \lambda \)):

Density (\( \rho_w \)):

Radius (\( R \)):

1. What is Capillary Rise Calculator?

Definition: This calculator computes the capillary rise height (\( h_c \)) of a fluid in a narrow tube due to capillary action, based on the fluid’s surface tension (\( \sigma \)), meniscus angle (\( \lambda \)), density (\( \rho_w \)), and the tube’s radius (\( R \)).

Purpose: It helps scientists, engineers, and researchers understand how high a fluid will rise in a capillary tube, useful in fields like fluid dynamics, biology (e.g., plant water transport), and materials science.

2. How Does the Calculator Work?

The calculator uses the following equation:

\( h_c = \frac{2 \cdot \sigma \cdot \cos(\lambda)}{\rho_w \cdot g \cdot R} \)

Where:

\( \sigma \): Surface tension of the fluid (in N/m, dyn/cm, lbf/in, or lbf/ft, default 0.0757 N/m for water);
\( \lambda \): Meniscus angle (contact angle, in degrees);
\( \rho_w \): Density of the fluid (in kg/m³, g/cm³, or lb/ft³, default 998.2071 kg/m³ for water);
\( g \): Acceleration due to gravity (9.80665 m/s²);
\( R \): Radius of the capillary tube (in mm, cm, or in);
\( h_c \): Capillary rise height (in m, cm, in, or ft);
Results are displayed with 3 decimal places (or scientific notation if less than 0.001).

Steps:

Enter the surface tension (\( \sigma \)) of the fluid and select the unit (N/m, dyn/cm, lbf/in, lbf/ft).
Enter the meniscus angle (\( \lambda \)) in degrees.
Enter the density (\( \rho_w \)) of the fluid and select the unit (kg/m³, g/cm³, lb/ft³).
Enter the radius (\( R \)) of the capillary tube and select the unit (mm, cm, in).
Click "Calculate" to compute the capillary rise height.
Change the result unit dropdown to convert the height to a different unit (m, cm, in, ft).

3. Importance of Capillary Rise Calculation

Calculating capillary rise is crucial for:

Fluid Dynamics: Understanding how fluids move in narrow spaces, such as in porous materials or microchannels.
Biological Systems: Explaining water transport in plants, where capillary action helps water rise against gravity.
Materials Science: Studying wetting properties and designing microfluidic devices or capillary-based systems.

4. Using the Calculator

Example 1: Calculate the capillary rise with \( \sigma = 0.0757 \, \text{N/m} \), \( \lambda = 0^\circ \), \( \rho_w = 998.2071 \, \text{kg/m³} \), \( R = 1 \, \text{mm} \), result in cm:

Surface Tension: 0.0757 N/m;
Meniscus Angle: 0° (cos(0) = 1);
Density: 998.2071 kg/m³;
Radius: 1 mm = 0.001 m;
\( h_c = \frac{2 \cdot 0.0757 \cdot \cos(0)}{998.2071 \cdot 9.80665 \cdot 0.001} \approx 0.0155 \, \text{m} \);
Convert to cm: \( 0.0155 \times 100 = 1.548 \, \text{cm} \);
Result: Capillary Rise = 1.548 cm.

Example 2: Calculate the capillary rise with \( \sigma = 0.00412 \, \text{lbf/in} \), \( \lambda = 30^\circ \), \( \rho_w = 1 \, \text{g/cm³} \), \( R = 0.1 \, \text{cm} \), result in in:

Surface Tension: 0.00412 lbf/in = \( 0.00412 \times (4.44822 \div 0.0254) \approx 0.072 \, \text{N/m} \);
Meniscus Angle: 30° (cos(30) ≈ 0.866);
Density: 1 g/cm³ = 1000 kg/m³;
Radius: 0.1 cm = 0.001 m;
\( h_c = \frac{2 \cdot 0.072 \cdot \cos(30)}{1000 \cdot 9.80665 \cdot 0.001} \approx 0.0127 \, \text{m} \);
Convert to in: \( 0.0127 \times 39.3701 \approx 0.501 \, \text{in} \);
Result: Capillary Rise = 0.501 in.

5. Frequently Asked Questions (FAQ)

Q: What is Capillary Rise?
A: Capillary rise is the height to which a fluid rises in a narrow tube due to capillary action, driven by surface tension and opposed by gravity.

Q: Why does the meniscus angle matter?
A: The meniscus angle (contact angle) determines how the fluid interacts with the tube’s surface—smaller angles indicate better wetting, leading to higher capillary rise.

Q: Can this calculator be used for any fluid?
A: Yes, as long as you know the fluid’s surface tension, density, and meniscus angle with the tube material.